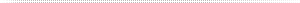By Tim Dugan, P.E., President, Compression Engineering Corporation
03/17/2017
Introduction
Based on my 28 years’ experience, I am an unapologetic “compressed air nerd”. But, I also understand vacuum systems. The reason I do is that I look at every problem from the fundamentals, not from rules of thumb. Any technical field develops a language and a set of “rules of thumb”. It is helpful to do this, to disseminate ideas and practices broadly and quickly. These ways of thinking get reinforced when they appear to “work”. However, this type of thinking tends to create pathways of thinking that are ruts. These ruts run deep in every field, particularly compressed air.
If you want to understand vacuum systems, you have to get out of the ruts, and slog through the mud and bounce over the rocks a bit. If you’re a “compressed air person”, think outside the box for a few pages with me. I am going to borrow some terms from the “pump people” to explain how vacuum systems are similar, yet different from compressed air systems. There are several ruts to get out of. Remembering what changes and what doesn’t, what is controlled, and how to design systems for optimal energy consumption.
What Changes and What Doesn’t: System Resistance Changes
Always start with the system. Pump people teach us to look at a system as an “equivalent orifice”, a resistance that flow and pressure are related to one another, and to develop a “system resistance curve” first. Both vacuum and compressed air systems are essentially a variable leak, a variable hole, with air moving from one pressure to another across it. This seems to be analogous to a variable flow demand. But be careful. The system is really just holes that open and close, or have variable sized holes (control valves). In some limited cases, flow control is part of the system, making it actually a flow-based demand. But that is uncommon. The aggregate of all these variable holes is the “system”. The system gulps what it wants, independent of the vacuum pumps or compressors attempting to serve it. For vacuum systems, air moves from constant ambient pressure to the vacuum pump inlet pressure. For compressed air system, it moves from the compressor’s roughly constant discharge pressure to ambient pressure.
In both cases, the system typically acts as a “choked orifice”. Air is trying to move through the orifice too fast, and is limited based on a maximum pressure ratio of about 53% for air. Basically, a shock wave exists at the point that air is trying to get into the system. For a choked orifice, mass flow is proportional to the inlet pressure. In layman’s terms, this means that if you double either the inlet pressure to the system, you get about double the flow – assuming that you can deliver it. In a vacuum system, you can’t change the “inlet pressure” to the system – it’s ambient pressure. But that’s just theory. You have to be able to magically increase or decrease mass flow to respond to that need to change pressure, and real vacuum pumps can’t do that without a VFD. Or you have to operate at widely ranging pressures, which compressors don’t do. More on that below.
Figure 1 shows a typical system curve for a vacuum system running at one constant load, or a set of “holes” open. The mass flow stops increasing at the “choked flow” vacuum level.
Figure 1. Typical System Resistance Curve for Vacuum System
Compressed Air Implications
- Gas density is fairly constant, because the air compressor’s discharge pressure only changes about 10% of set point.
- The only variable that influences mass flow is pressure, but far less than in a vacuum system. Only about 10%. Thus, you can often neglect the impact of pressure on flow for typical compressed air systems.
Vacuum System Implications
- Since there is a big range of pressure difference (inlet to ambient) that can exist in a vacuum system - often over 20% of an atmosphere or 40% of set point - mass flow is highly related to vacuum level, and vice-versa.
- Since gas density in vacuum systems can change dramatically as the pressure/vacuum changes, there is a big impact of mass flow on density, and density on mass flow.
- Pay attention to the balance of pressure and density, and its impact on flow.
What Changes and What Doesn’t: Compression Element Size Doesn’t Change
This might seem obvious, but it’s important to understand. In a real system, you are stuck with the iron that you have, unless you are designing a new system. Thus, air compressors and vacuum pumps have to be oversized. Even if you have flexibility on paper now, you will be stuck in the future. For simplification in this article, I will assume we are looking at “positive displacement” vacuum pumps and compressors. Those types have a fairly constant volume flow rate at the inlet, at a given speed. Slip and pressure differential across the compression element don’t affect it that much (less than 5%).
All you can do to make the most of a system is to attempt to match the right air compressor or vacuum pump to the right system, which is difficult because you have a widely varying “system resistance”. The compressor or vacuum pump has to be oversized for average demand, or the system will crash at max demand.
Vacuum pumps and air compressors are sized for inlet flow, at full speed and a particular pressure ratio that is optimal. For instance, 1,000 “acfm” and 100 psig for a compressor. That is 1,000 cubic feet per minute at the inlet, independent of density, compressing from ambient pressure to 100 psig. It just takes a scoop of 1,000 ft3 volume every minute, and squeezes it 7.8 times. Typically a curve is not provided, just a full capacity data sheet. If one is, it shows power versus flow, not flow versus pressure. See Figure 1 for an example. Pressure is magically relatively constant, so the engineer doesn’t think about how it impacts on the flow capacity of the compressor, or how it balances against the system.
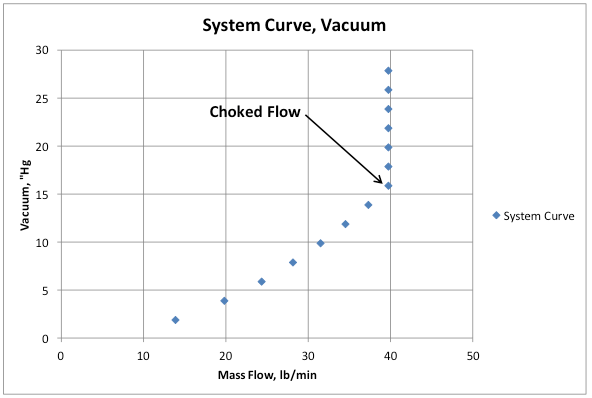
A 1,000 “icfm” vacuum pump could use the same compression element as the 1,000 acfm compressor, or one modified with a different compression ratio to optimize for vacuum system operation, 1,000 icfm at 28”Hg for instance. It would have a much smaller motor and a larger separator (if lubricated). Its performance would look flat as a pancake from 10”Hg to about 25”Hg, and decline slightly after that. See Figure 2 for an example. But don’t be fooled. Your real system will not require 1,000 icfm in all vacuum ranges. Recall that the system is just a hole. The vacuum pump will pull down until it balances at whatever pressure differential/density balances with the system resistance at the time.
The vacuum pump curve and system curve can both be shown together, Figure 2. Without using controls, the operating point is the intersection of the vacuum pump curve and system curve.
Figure 2. One Vacuum Pump Running Against Demand
What Controls What?
In an ideal system, you would control based on optimal process effectiveness. If the process is mass-flow sensitive, then it should be mass-flow control, throughout. If it is pressure-sensitive, then it should be pressure-based. In reality, it is very difficult to control vacuum and compressed air systems by a mass-flow set point. The instrumentation, controls, and mechanical limits of mass-flow control make it applicable to a limited range of applications, usually process compressors/vacuum, and not general plant air vacuum. For this article, we are discussing general plant systems. These systems are pressure-controlled in practice, whether the system needs mass-flow controlled or pressure controlled. But the system does what it does all on its own, and is the “feedback loop” that dominates the actual operation.
Compressed Air Implications
System demand is independent of pressure within the air compressor’s operating range. System demand = A, pressure = B, and flow = C. Control happens A to B to C, essentially A=>C. There is a small feedback between pressure and system demand (C => A), but not much. System demand changes pressure, just a small amount up or down on the “system curve”, the control system cuts back or increases compressor flow to match system flow – by stabilizing pressure. As an example, an inlet modulating compressor uses a proportional pilot valve to control its inlet valve to a given plant pressure, and a VFD control controls speed to maintain a plant’s pressure.
Vacuum System Implications
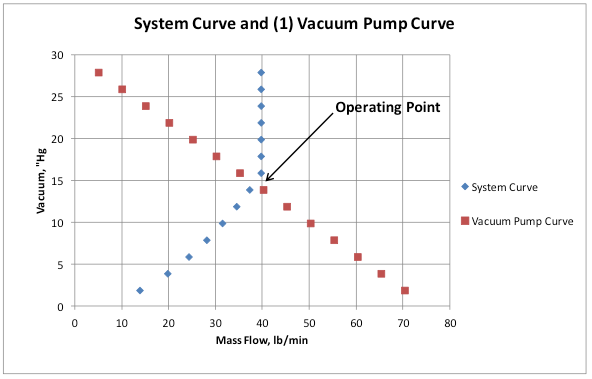
System demand is dependent on pressure in a vacuum pump’s operating range. Typically, pumps are pulling too low of a vacuum, to be safe, and that lower vacuum is causing a false demand on the vacuum pump. Thus, A =>B => C => A, and it reaches a balance. Even if mass flow is choked, the lower vacuum causes a higher vacuum pump inlet flow (icfm) to hit that same mass flow, and that takes more power. See Figure 3 for the same system resistance as shown in Figure 1, but with two vacuum pumps running. The system will just balance at a lower vacuum, 22”Hg versus 15”Hg. Power will be about double, and the process wouldn’t even know that the other vacuum pump was on. Unlike a compressed air system that would over-pressurize and cause a compressor to unload, the vacuum pumps essentially “self-throttle” against the system.
Figure 3. Impact of Running Two Vacuum Pumps on Same Demand
Design for Optimal Energy Consumption: Determine the Vacuum Level and Flow Actually Needed
Start at the process, the part that creates the demand, the “holes”. There are multiple types. Fixed and varying demand, pump-down and hold, and constant flow. For instance, in a CNC routing table’s “hole” is the sum of a bunch of tiny holes that pull air through the table to hold a work piece down. It is a varying demand because the flow only occurs when the table is not covered, and many different types of work pieces cover the table, leaving a varying area uncovered. In a chemical process, the “hole” is usually a control valve maintaining a particular process variable, and the flow is fairly constant. In a robot application, the “hole” is the suction cup that has a very small volume, and holds a piece to block the hole, zero flow, then drops it and has a high flow.
If you can perform an analysis of all the demands, the best way is to turn them all into equivalent orifices or CVs (a valve sizing term, similar to hole size, but more technical). Then, using the minimum required vacuum level for the system (the lowest vacuum needed for all), aggregate them and develop a peak and average flow, using the orifice flow formula, up to the choked flow level. An example is in Table 1, for just one 1.783” diameter hole, equivalent to a 1,000 icfm demand at 14”Hg. Obviously a real plant isn’t one hole. This is the equivalent of all the demands. These formulas are available in a variety of toolboxes online. If you do this in a spreadsheet, it would have more columns than these.
Table 1. System Demand Calculations, Max Demand
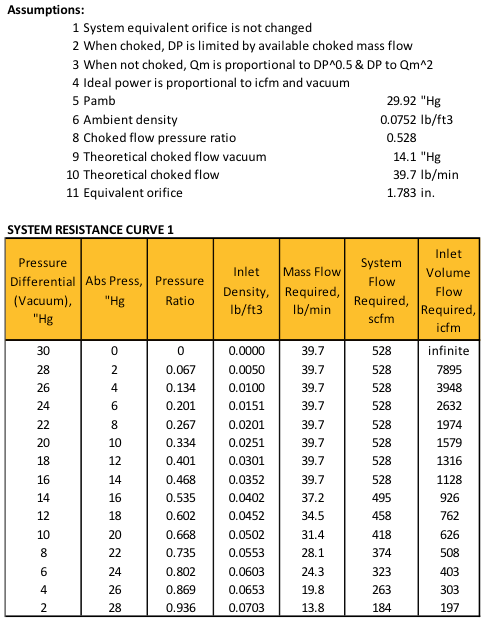
For this example, let’s assume the required vacuum is 15”Hg, and max demand is 1,000 icfm. If the average and minimum levels were calculated, let’s assume them to be 600 and 200 icfm at 15”Hg.
Design for Optimal Energy Consumption: Match Vacuum Pumps Against Demand, Full Range
With a variance of 5:1 max/min flow, typical in automation systems, one large 1,000 icfm vacuum pump would be inefficient. In this case, a multiplex is recommended. In many production systems, dedicated, independent vacuum pumps are used, one per production system. This is generally OK if the pump is shut off often or small. But for systems that run often, it leads to a dead-load dominated system. Consolidation and automation with a multiplex vacuum pump system is recommended. Sequencing controls can be used to maintain vacuum within a differential, and pumps can be staged. More details on system design will be in a forthcoming article.
Conclusions
- Understanding system resistance is important to optimizing vacuum systems. It is the “equivalent hole” that the system leaks in from atmosphere. It is the relationship between flow and vacuum in any system, so it is important to understand it first.
- Vacuum pump size is expensive to change, so match it well to demand. Consider multiplex and sequenced system designs for varying demands to reduce dead-load power.
- Vacuum level controls system flow, and pump size draws a system to a deeper vacuum than needed, so false demand is easy to create. Optimizing controls for the required vacuum minimizes that false demand.
For more information, contact Tim Dugan, tel: 503-520-0700, email: Tim.Dugan@comp-eng.com, or visit www.comp-eng.com.
To read more Vacuum Technology articles, please visit www.blowervacuumbestpractices.com/technology/rough-vac.